Graph Representation Learning是GraphSAGE第一作者William Hamilton的新书,下载地址https://www.cs.mcgill.ca/~wlh/grl_book/files/GRL_Book.pdf
Background and Traditional Approaches
本章提供了一些方法论背景,介绍了在现代深度学习方法问世以前,基于图的机器学习使用了哪些方法。作者首先介绍了基本的图统计、核方法以及它们在节点和图分类任务中的使用。然后作者在书中介绍并探讨了用于测量节点邻居之间重叠的方法,最后简要介绍了使用拉普拉斯(Laplacians)进行谱聚类。
在介绍图表示学习和图深度学习的概念之前,有必要提供一些方法背景和上下文。在现代深度学习方法问世之前,在图上使用哪种类型的机器学习方法?在本章中,我们将对图上的传统学习方法进行非常简短且有针对性的浏览,在此过程中未这些方法论方法的更彻底处理提供指示和参考。本章还将介绍图分析中的关键概念,这些概念将为以后的章节奠定基础。
我们的行程将大致与图上的各种学习任务保持一致。我们将从基本图统计、核方法及其在节点和图分类任务中的使用开始讨论。接下来,我们将介绍并讨论用于测量节点邻域之间重叠的各种方法,这些方法构成了用于关系预测的强大启发式方法的基础。最后,我们将通过使用图拉普拉斯算子对谱聚类进行简要介绍来结束本背景部分。谱聚类是对图进行聚类或社区检测方面研究最深入的算法之一,这些关键的数学概念在本书中将反复出现。
Graph Statistics and Kernel Methods
使用图数据进行传统分类的方法遵循在深度学习出现之前流行的标准机器学习范式。我们首先根据启发式函数或领域知识提取一些统计信息或特征,然后将这些特征用作标准机器学习分类器(例如,逻辑回归)的输入。在本节中,我们将首先介绍一些重要的节点级功能和统计信息。在此之后,我们将讨论如何将这些节点级别的统计信息推广到图级别的统计信息,以及如何扩展到设计基于图的核方法。我们的目标是引入各种启发式统计数据和图形属性,这些属性通常用作应用于图的传统机器学习管道中的功能。
Node-level statistics and features
继Jackson之后,我们将通过一个简单(但著名)的社交网络(15世纪佛罗伦萨婚姻网络)来激发我们对节点级统计和功能的讨论(图2.1)。这个众所周知的社交网络是Padgett和Ansell在1993年的工作,他们利用这个网络说明了统治佛罗伦萨政治的Medici家族(描绘在中心附近)的权力上升。政治婚姻是在Medici时代巩固权力的的重要途径,因此这种婚姻联系网络在很大程度上编码了这段时期的政治结构。
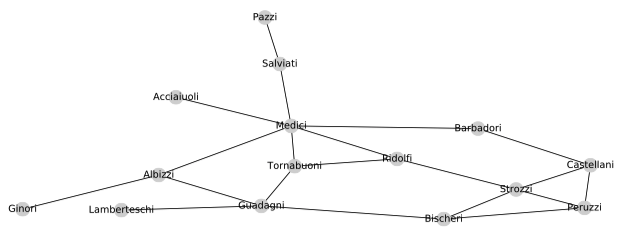
为了我们的目标,我们将从机器学习的角度考虑这个网络和Medici家族的兴起,并提出一个问题:机器学习模型可以用哪些特征或统计数据来预测Medici家族的兴起?换句话说,Medici节点的哪些属性或统计数据将其与图的其余部分分开?而且,更笼统地说,有什么有用的属性和统计信息可用来表征此图中的节点?
原则上,我们下面讨论的属性和统计数据可用作节点分类模型中的特征(例如,用作逻辑回归模型的输入)。当然,我们无法在像佛罗伦萨婚姻网络一样小的图上实际训练机器学习模型。但是,考虑可用于区分这种现实网络中的节点的属性种类依然是可说明的,而且我们讨论的属性通常可用于各种节点分类任务。
节点的度 最明显直接的节点特征是度(degree),对一个节点$u \in \mathcal{V}$来说,通常将其度表示为$d_u$,并简单地将其计算为入射到节点的边的数量:
$d_u = \sum_{v \in \mathcal{V}} \mathbf{A}[u, v]\tag{2.1}\label{degree}$
注意,在有向图和加权图中,可以通过对公式$\eqref{degree}$中的行或列求和来区分不同的度,例如,对应的输出边或输入边。通常,节点的度是要考虑的基本统计信息,并且通常是应用于节点级人物的传统机器学习模型中的最有用的功能之一。
在佛罗伦萨婚姻说明图中,我们可以看到,度数确实是区分Medici家族的一个好特征,因为它在图中具有最高的度数。但是,他们的度仅比Strozzi和Guadagni两个家族高出2。还有其他或更容易区分的特征帮助区分Medici家族和其他图吗?
Node centrality
节点度只是衡量一个节点有多少邻居,但这并不一定足以衡量图中一个节点的重要性。在许多情况下(例如佛罗伦萨婚姻图),我们可以从其他更有效的节点重要性度量中受益。为了获得更强大的重要性度量,我们可以考虑各种所谓的节点中心性度量,这些度量可以在各种节点分类任务中形成有用的功能。
普遍性和重要的中心度度量是所谓的特征向量中心度。度只是衡量每个节点有多少个邻居,而特征向量中心性也考虑到了节点的邻居有多重要。特别的是,我们通过递归关系定义节点的特征向量中心度$e_u$,其中节点的中心度与其邻居的平均中心度成正比:
$e_u = \frac{1}{\lambda} \sum_{v \in \mathcal{V}} \mathbf{A}[u, v] e_v, \forall u \in \mathcal{V}\tag{2.2}\label{centrality}$ 其中$\lambda$是一个常数。用向量重写该方程,将$\mathbf{e}$作为节点中心点的向量,我们可以看到其定义了邻接矩阵的标准特征向量方程:
$\lambda \mathbf{e} = \mathbf{A} \mathbf{e}\tag{2.3}\label{adjacency}$ 换句话说,满足公式$\eqref{adjacency}$中的递归的中心度对应于邻居矩阵的特征向量。假设我们需要正的中心值,我们可以应用Perron-Frobenius定理进一步确定中心值$\mathbf{e}$的向量是由对应于$\mathbf{A}$的最大特征值的特征向量给出的。
Perron-Frobenius定理是线性代数的节本结论,由Oskar Perron和Georg Frobenius单独证明。完整定理有很多含义,但是出于我们的目的,定理中的关键断言是任何不可约方针都具有唯一的最大实特征值,这是唯一可以选择其对应特征向量具有严格正分量的特征值。
特征向量中心性的一种观点是,它对图上无限长的随机游动中访问一个节点的可能性进行排序。该观点可以通过考虑使用幂迭代来获得特征向量中心值来说明。也就是说,由于$\lambda$是$\mathbf{A}$的特征向量,我们可以通过幂迭代来计算$\mathbf{e}$
$\mathbf{e}^{(t+1)} = \mathbf{A} \mathbf{e}^{(t)}\tag{2.4}$ 如果我们从向量$\mathbf{e}^{(0)}=(1, 1, \cdots, 1)^{\top}$开始迭代,那么我们可以看到,在第一次迭代之后,$\mathbf{e}^{(1)}$将包含所有节点的度数。通常,在迭代次数$t \geq 1$时,$\mathbf{e}^{(t)}$将包含到达每个节点的长度为$t$的路径的数量。因此,通过无限次地迭代此过程,我们得到一个分数,该分数与在无限长的路径上访问节点的次数成正比。节点的重要性、随机游走和图邻接矩阵的谱之间的联系将在本书的后续各节和各章中经常提到。
回到以佛罗伦萨婚姻网络,如果我们在该图上计算特征向量中心值,我们可以看到还是Medici家族的影响最大,归一化值为0.43,第二高值为0.36。当然,我们还可以使用其他集中度度量来表征该图中的节点——其中一些相对于Medici家族的影响力更为明显。这些包括相互之间的中心性(它衡量一个节点位于两个其他节点之间的最短路径上的频率)以及邻近性中心性(它衡量一个节点与所有其他节点之间的平均最短路径长度)。Newman对这些措施做了详细的综述。
The CLustering coefficient
重要性和中心度等重要指标对于区分著名的Medici家族与其他佛罗伦萨婚姻网络显然很有用。但是,对于区分图形中其他节点有用的功能又如何呢?例如,图中的Peruzzi和Guadagni节点具有非常相似的度数(3 v.s. 4)和相似的特征向量中心点(0.28 v.s. 0.29)。但是,从图2.1可以看出,这两个家族之间存在明显的差异。Peruzzi家族处于相对紧密的家族集群中,而Gradagni家族则扮演着更像“星星”的角色。
可以使用聚类系数的变化类衡量这种重要的结构区别,聚类系数用于衡量节点本地邻域中闭合三角形的比例。聚类系数的局部变量计算如下:
$c_u = \frac{\vert (v_1, v_2) \in \mathcal{E}: v_1, v_2 \in \mathcal{N}(u)\vert}{d_{u} 2}\tag{2.5}$ 此等式中的分子计算节点$u$的邻居之间的边数(我们使用$\mathcal{N}(u)=\{v\in \mathcal{V}:(u, v) \in \mathcal{E} \}$表示节点的邻域。分母计算出节点的邻居中有多少对节点。
聚类系数的名称源于以下事实:它可以测量节点邻域的聚类紧密程度。聚类系数为1表示节点的所有邻域也是彼此的邻居。在佛罗伦萨婚姻图中,我们可以看到一些节点高度聚类(例如,Peruzzi节点的聚类系数为0.66,而其它节点(例如Guadagni节点)的聚类系数为0)。就中心性而言,存在许多中心系数的变体(例如,考虑有向图)的数量,Newman也对其进行了详细调查。整个社会和生物学科学中,现实世界网络的一个有趣而重要的特性是,它们的聚类系数往往比随机采样的边会产生的聚类系数要高得多。
Closed triangles, ego graphs, and motifs.
查看聚类系数的另一种方法(而不是衡量局部聚类的一种方法)是,计算每个节点的本地邻域内的封闭三角形的数量。用更精确的术语来说,聚类系数与节点的自我中心网络(ego graph)中(即包含该节点,其邻居以及该节点中节点之间的所有边的子图)中的实际三角形数与可能的总三角形数之比有关。
这种想法可以推广到对节点的自我中心网络中的任意图或子图进行计数。也就是说,我们不仅可以考虑三角形,还可以考虑更复杂的结构,例如特定长度的循环,并且可以通过计数这些不同的图案在其自我中心网络中出现的频率来表征节点。实际上,通过以这种方式检查节点的自我中心网络,我们可以将计算节点级统计信息和特征的任务从本质上转变为图形级任务。因此,我们现在将注意力转向这个图级问题。
Graph-level features and graph kernels
到目前为止,我们已经讨论了节点级的各种统计信息和属性,这些统计信息和属性可以用作节点级分类任务的功能。但是,如果我们的目标是进行图集分类怎么办?例如,假设我们得到了代表分子的图数据集,而我们的目标是根据这些分子的图形结构对它们的溶解度进行分类。我们将如何做?在本节中,我们将简要介绍为此类任务提取图形级特征的调查方法。
我们在这里调研的许多方法都属于图核方法的一般分类,图核方法是设计可用于机器学习模型的图或隐式核函数的特征的方法。我们将仅设计在这个大区域内的一小部分方法,并且我们将专注于提取显式特征表示的方法,而不是定义图之间的隐式核(即相似性度量)的方法。